Morse Code vs. ASCII Code
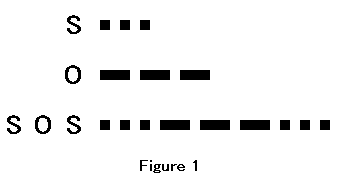
First, we shall consider Morse code, which is perceptible digital information. Morse code consists of dots and dashes. A dot represents a short sound and a dash represents a long sound. The speed of Morse code is measured in words per minute (WPM) or characters per minute. Figure 1 shows Morse code for S, Morse code for O and Morse code for SOS.
The Wasp and the Cricket
. . . for by the beginning of September the Wasp must begin to dig her burrows and search for game for her family.If we look at the Cricket a week, two weeks, or even longer after the murder, we shall see the abdomen moving slightly, a sign that he is still alive.
The yellow-winged Wasp is not content with comparatively defenseless Beetles and Caterpillars; she hunts the powerful Cricket.
Notice, therefore, the precautions the Wasp takes before setting her sting in motion. She turns the Cricket upon his back so that he cannot use his hind-legs to escape. She controls his spurred legs with her fore-feet, so that he cannot kick her; and she keeps his jaws at a distance with her own hind-legs. She makes him motionless by grasping one of the threads at the end of the abdomen. An athlete, an expert wrestler, could not do better.
Consider also her science. She wishes to paralyze the prey without killing it, so that it will remain in a fit condition for food for her babies for many weeks. If she should leave the Cricket any power of motion, it would knock the eggs off; if she killed it entirely, it would decay. How does she produce this paralysis? She does just what a surgeon would advise her to do: she strikes the nerve-centers that set the legs in motion.
After she has paralyzed her Cricket, she drags it into her burrow. When she has gathered three or four Crickets, she lays an egg and closes the burrow. Although she has not met the Cricket until then, she can hunt the cricket with skill at the first time, and she already knows the location of Cricket's nerve-centers that set the legs in motion. That is to say, she must acquire these skills before birth. Additionally, the entire behavioral sequence is fixed. Therefore, this sequential behavior seems to be completely programed by DNA.
On the contrary, a resident must train hard for a long time to be a surgeon. Also, a wrestler must train muscles, and he must fight a battle repeatedly in order to master wrestling skills. So, it is difficult for us to master skills. For Example, if an unskilled resident saw a surgery, he could not do the same surgery.
We cannot easily master another person's skills because our perception is inaccurate. In contrast, the technique of the wasp is completely accurate because natural selection endowed the wasp with these skills. This is the power of digital information. It can be copied accurately, and it can be the object of natural selection.
The Origin of Mathematical Concept
Plato says that the natural number one cannot be perceived by any sense. We can see Arabic numeral one, but it is not the natural number one itself. We can hear only the pronunciation of one, but it is not the natural number one itself. So we cannot directly see or hear the pure natural number one itself. Even if we use any kind of sense, we cannot recognize the pure natural number one itself. This is the mysterious problem. That is, we use natural numbers routinely, but we cannot recognize the pure natural number one itself through any sense organ. Plato says about this problem using the analogy of the divided line "Now take a line which has been cut into two unequalparts, and divide each of them again in the same proportion, and suppose the two main divisions to answer, one to the visible and the other to the intelligible, and then compare the subdivisions in respect of their clearness and want of clearness". Then, we shall quote paragraphs in Republic Ⅵ about mathematical concepts:Then I will try again; you will understand me better when I have made some preliminary remarks. You are aware that students of geometry, arithmetic, and the kindred sciences assume the odd and the even and the figures and three kinds of angles and the like in their several branches of science; these are their hypotheses, which they and everybody are supposed to know, and therefore they do not deign to give any account of them either to themselves or others; but they begin with them, and go on until they arrive at last, and in a consistent manner, at their conclusion?In the analogy of the divided line, Plato divides human knowledge into visible things and intelligible things. Mathematical concepts are intelligible things and geometrical figures are visible things. Mathematicians use both things. However, if we can acquire knowledge only through senses, the next question arises. When did we acquire mathematical concepts? In Phaedo, Socrates answers:
Yes, he said, I know.
And do you not know also that although they make use of the visible forms and reason about them, they are thinking not of these, but of the ideals which they resemble; not of the figures which they draw, but of the absolute square and the absolute diameter, and so on --the forms which they draw or make, and which have shadows and reflections in water of their own, are converted by them into images, but they are really seeking to behold the things themselves, which can only be seen with the eye of the mind?
Then before we began to see or hear or perceive in any way, we must have had a knowledge of absolute equality, or we could not have referred to that the equals which are derived from the senses-for to that they all aspire, and of that they fall short?So, I understand Socrates's statement. However, the important question is remaining. How did we acquire mathematical concepts before birth? The Ancient Greeks could not solve this problem because they did not know the imperceptible entity. Nowadays, I shall propose the answer of this problem. I point out the fact that we know many imperceptible entities now. For example, the computer signal cannot be perceived by any sense, but it is the substantial entity. Also, a DNA base is the imperceptible entity. Before computer age, a DNA base was the closest entity to the natural number one, which is imperceptible, indivisible, invariable and equal to each other. Using DNA bases, natural selection wrote mathematical concepts in our genes. Therefore, DNA bases are relaying points between visual things and intelligible things. Moreover, a DNA base is the candidate of the substance of the natural number one. Because a DNA base has close properties to the natural number one, mathematical concepts may be derived from these properties of a DNA base.
That, Socrates, is certainly to be inferred from the previous statements.
And did we not see and hear and acquire our other senses as soon as we were born?
Certainly.
Then we must have acquired the knowledge of the ideal equal at some time previous to this?
Yes.
That is to say, before we were born, I suppose?